横戸台の小さな個別学習塾【県塾（けんじゅく）】。超基礎から超難問まで、お子さまのレベルに合った学習を行っております。

先日行われた、首都圏模試の小６の算数を

ご紹介します

『最近の中学入試対策問題って、どんなの？』

と、興味のある方は、ご自分で解いてみてください

『なあんだ、馬鹿にすんなよ。

小学生の問題なんかやってらんないよ。』

・・・・

ちょっと、そこのあなた！

大学受験を目指す高校生でも

解けないお子さんが沢山、沢山いますからね

最近は

中学受験、高校受験、大学受験といった

垣根を取っ払った問題が数多くあるようです

[１]　１以上の整数は全部で何通りできますか

[２]　６の倍数は全部で何通りできますか

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

では、下に解法を載せます

　(設問の[２]は省略いたします)

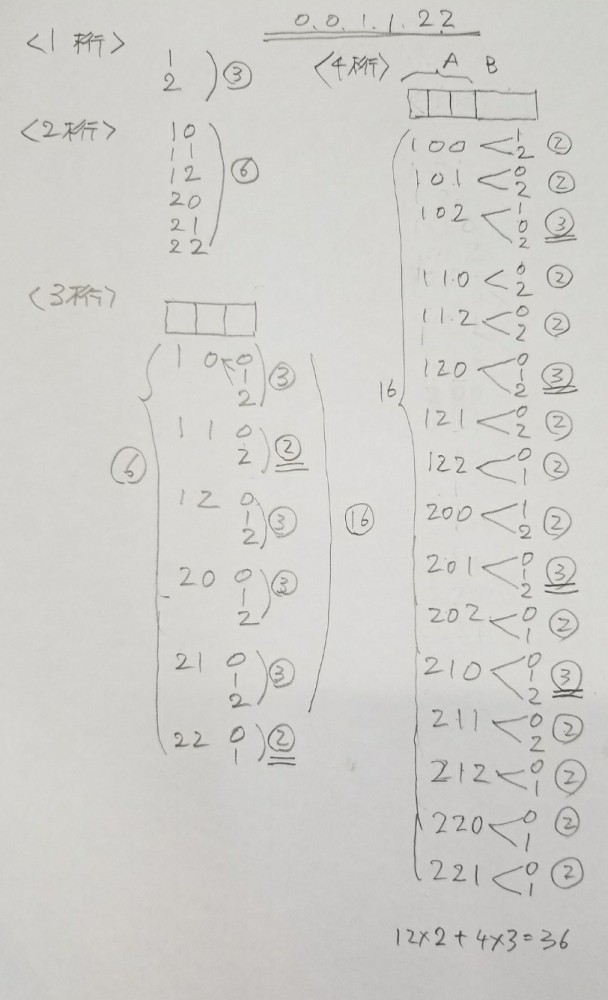
①『まず１ケタの整数は何個あるか』を

原始的に解いてください

・・・これは簡単でしょう　・・・答えは３通り

②『次に２ケタの整数は何個あるか』を

原始的に解いてください

・・・これも簡単でしょう　・・・答えは６通り

③そして次は３ケタです

・・これも簡単でしょう　・・・答えは１６通り

④いよいよ次は４ケタです

これまでのようにただ原始的に考えていては

時間がかかり過ぎます

ちなみに、③で求めた数字が

４ケタの頭の部分に来ると考え

あとは、一のケタ（位）の部分に

どんな数字が来るかを考えます

そこで『何か規則性は無いかな』と

考えてみましょう

とはいえ、ここでも

原始的思考が基本です

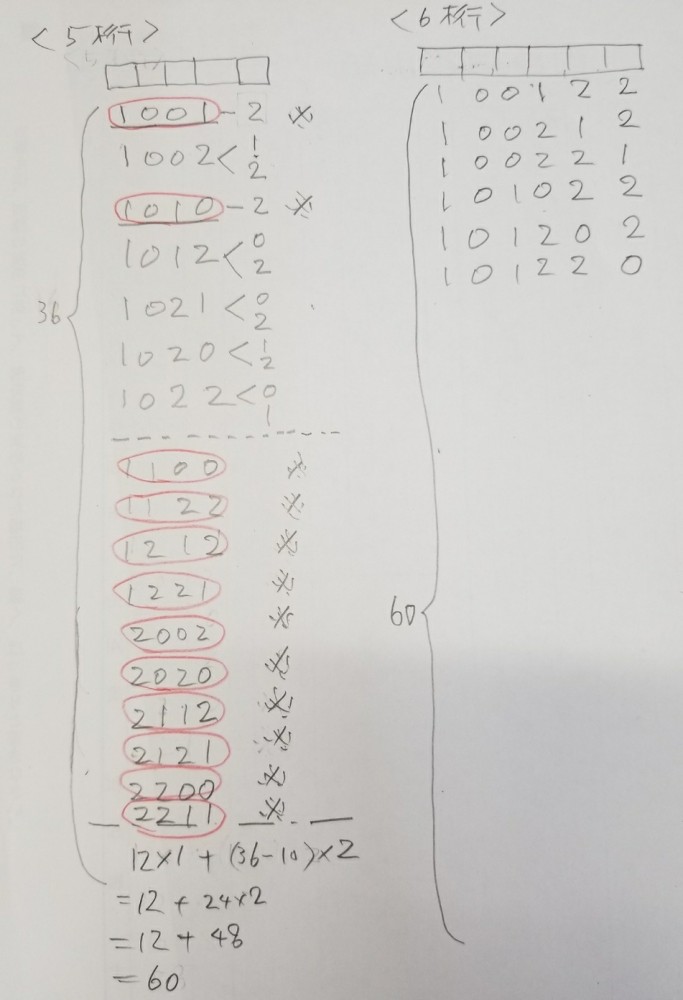
⑤次は５ケタです

次も④同様に頭の部分は④を使い

一のケタ（位）の部分についてだけ

考えます

同じ数字が２セットづつの数字と

それ以外の数字に分けられると

気付くと、

効率よく解けます

あとは、省略しますが

この問題が

そっくりこのまま今後も出題される可能性はゼロです

大切なのは

その都度、自分で

絵柄をイメージできるか？また

規則性を見つけられるかどうかです

この種の問題形式は入試問題として

今後、継続的に出題されることだけは

間違いないでしょう

なお、最近の公立高校の数学においては

こういった、『公式を使わない』新傾向の

問題が大問【６】あたりで必ず出題されています

追記）

今日、この問題を

中学３年生全員で解いてみました

美しい集中力です

そして

結果は、上々でした

嬉しい誤算でした